I. Preamble
Machine learning models can be complex and difficult to understand. In my last Epsilon essay, we looked at LIME for model interpretability. In this essay, we will be attending to SHapley Additive exPlanations, SHAP for shorts.
In brief, SHAP values help explain model predictions by showing how each feature contributes to the model output. SHAP values build on top of Shapley values from game theory.
In this note, I will first explain Shapley values and then show how they are extended to create SHAP values, specifically Kernel SHAP.
I should also say that one of the reasons (out of many others) SHAP is desirable is because it has both local and global interpretation capabilities.
II. Shapley Values
Shapley values were first proposed by Lloyd Shapley in the 1950s as part of his game theory research. The basic idea is that it gives a solution to fairly distribute gains among a group of players who are working together in a game.
An example is in order, a completely hypothetical one in this case.
Say I have coached a team with 4 players, for ease, let’s call them players A, B, C, and D. Now, say they won a big competition that will go un-named by 100 points, and won a $1M prize money.
I must now figure out how to share the hefty prize money amongst the players – and this is important –according to their contributions to the game.
How do we solve this problem, again, what we want here is a fairly axiomatic principle to distribute the payout.
Well, we need to know the impact of each player. This can be done by building a coalition of subsets of players, and figuring out the number of points those subsets of players will generate.
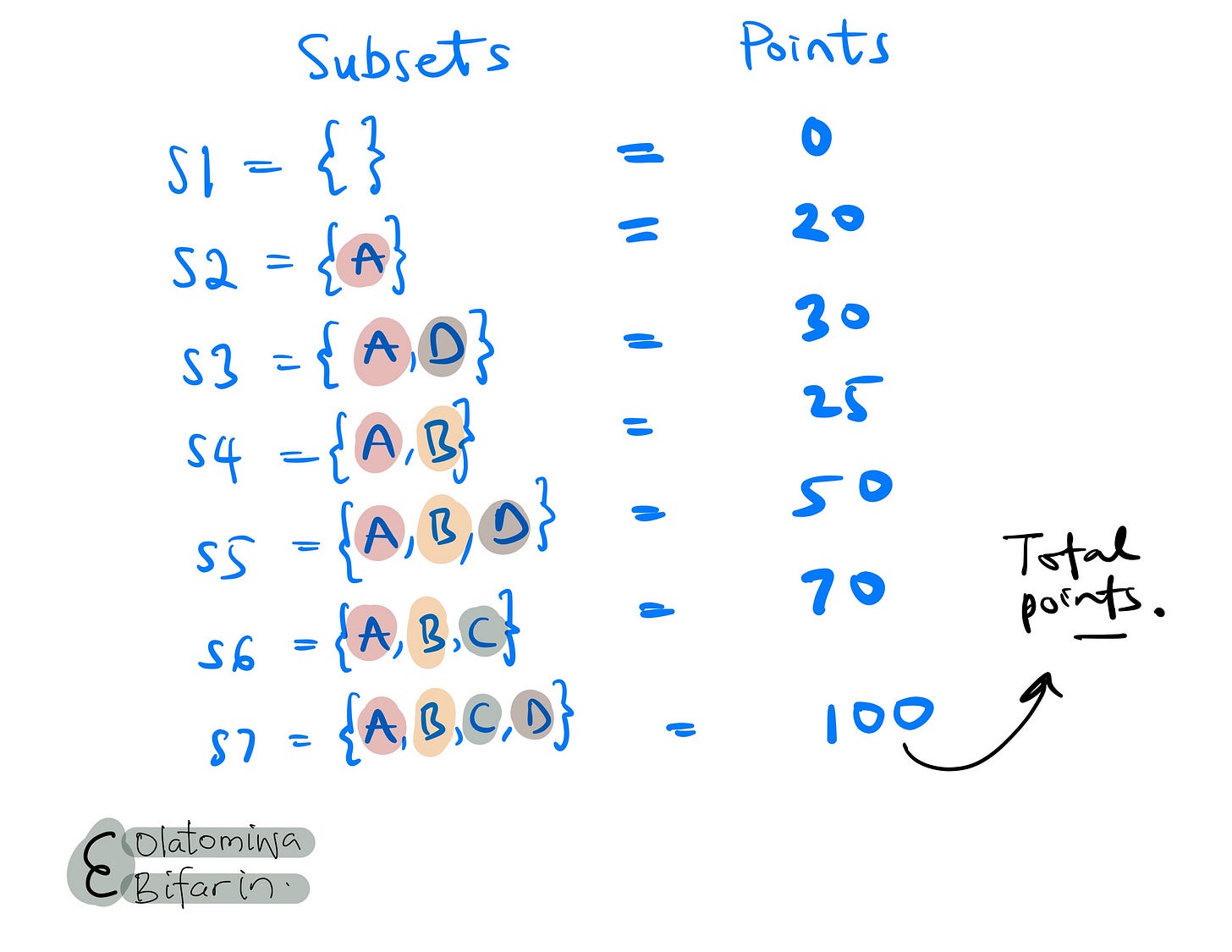
There are 16 possible subsets in total (4C0+4C1+4C2+4C3+4C4 = 16), however, let me illustrate with just a few subsets, focusing on player D.
Above, I show the total number of points earned from each subset of players.
Homing in on player D: we will pick subsets that include and exclude player D in order to estimate the impact of the player. In essence, the marginal contribution of player D to each of those coalitions (I will continue to use coalition in place of subset).
In the meantime, we can compute the same calculations for S2 and S3, and for S6 and S7. By doing this, we will be on a right path to figure out marginal contribution of player D to the game.
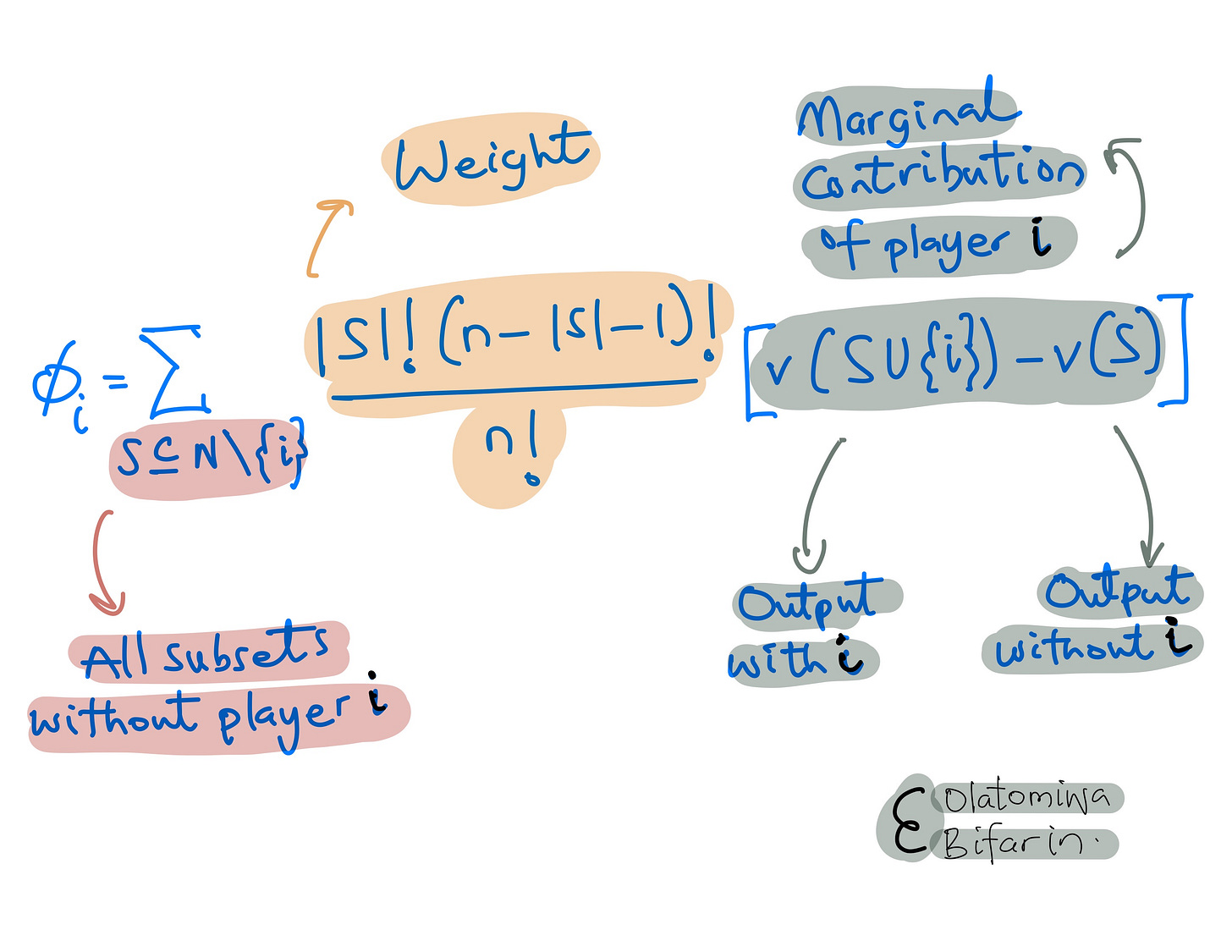
This is what the Shapley Value is. To generalize, take the following equation:
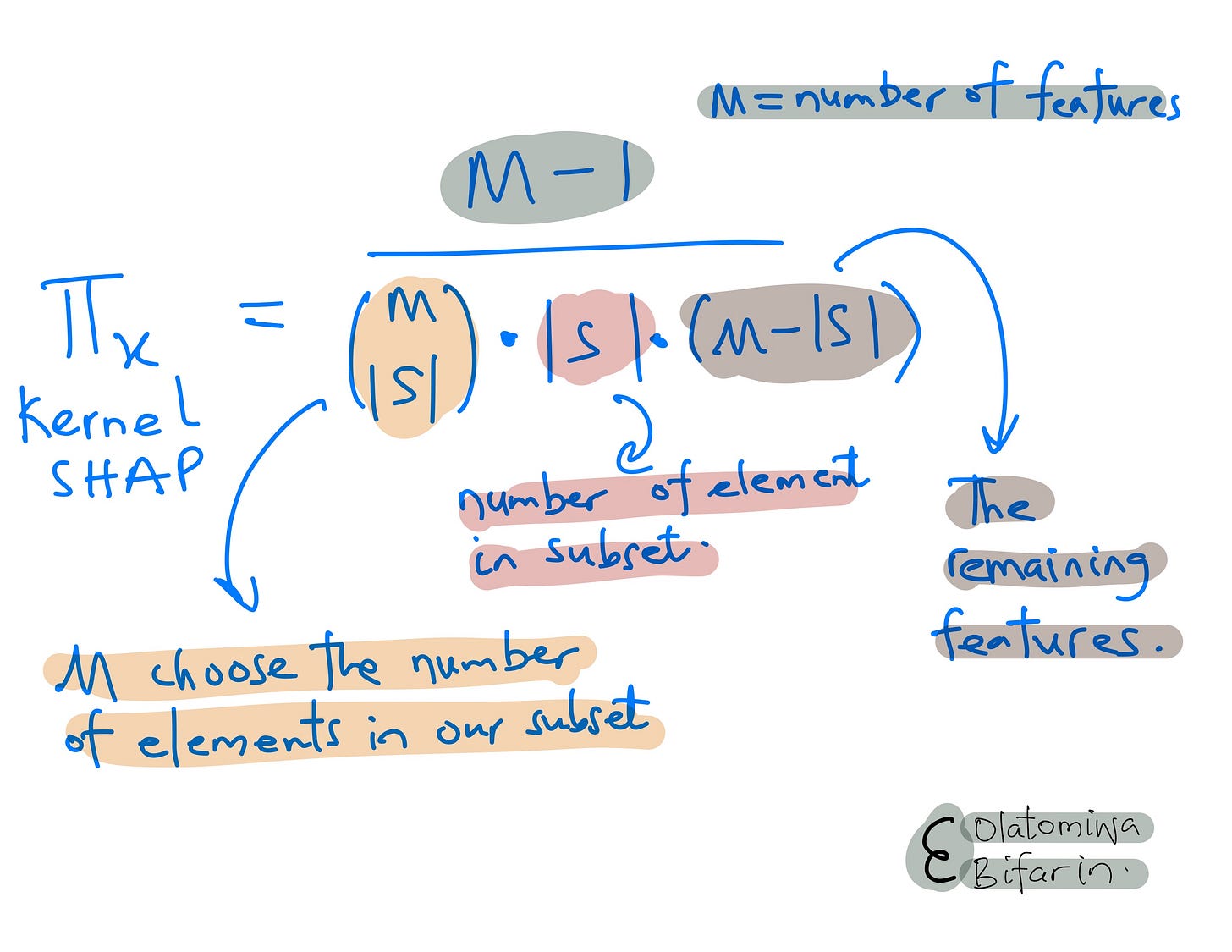
The weight is an important component to touch on briefly:
If you look more closely at the impact of the weight in this computation above, you will notice that if we have larger elements in the subsets, the impact will be much larger.
And why is Shapley value consequential?
It is because it is a unique solution that satisfies the axioms of symmetry, null effect, and additivity.
In brief:
Symmetry: Players contributing equally get equal values.
Null player: Players not contributing get zero value.
Additivity: For independent games, values add up.
III. Kernel SHAP: From Shapley Values to SHAP
In the context of machine learning, Shapley Values are used to determine the importance of each feature in a prediction.
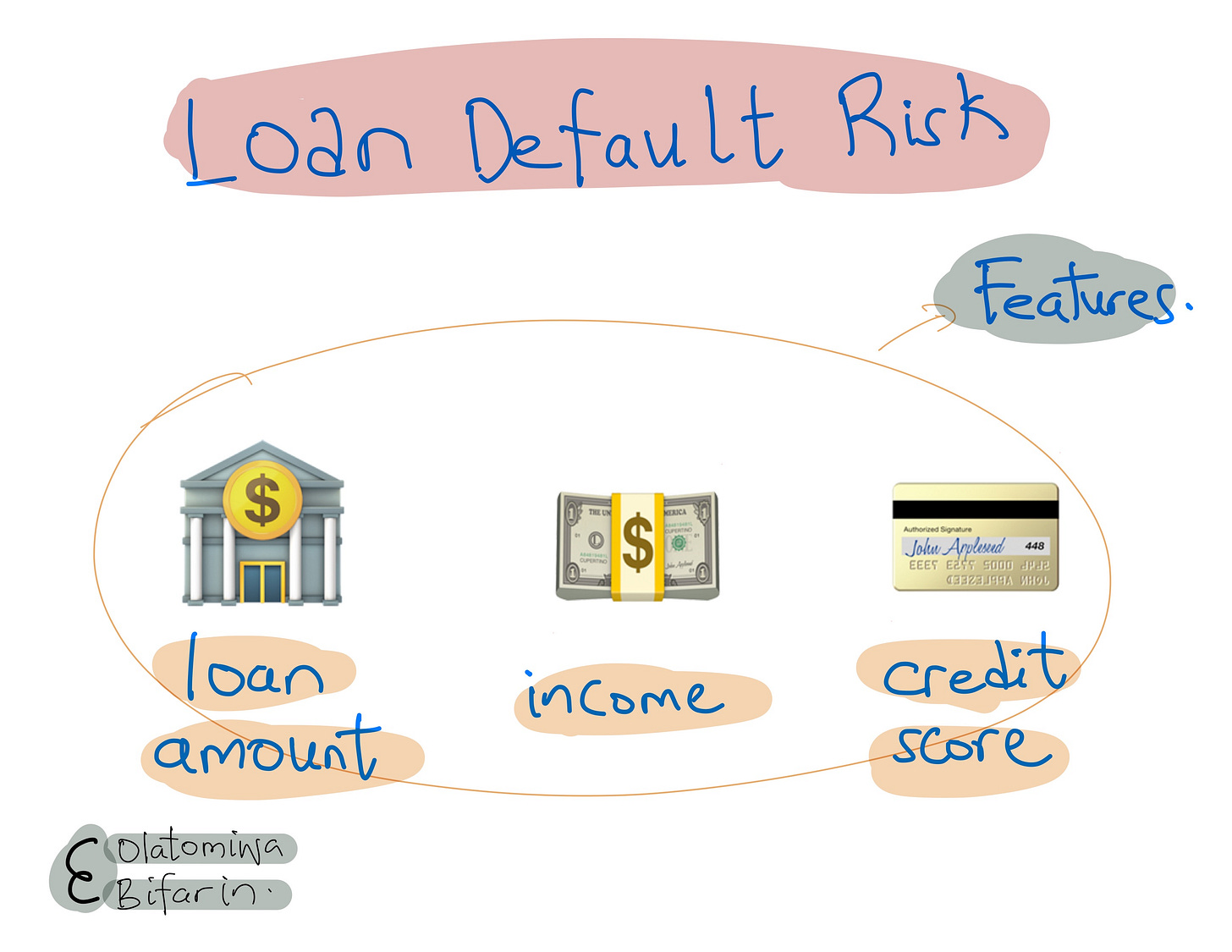
For example, if a model is predicting loan default risk based on features like income, credit score, and loan amount, the Shapley Value of the "income" feature would tell us how much the income feature contributes to the model's prediction, on average, across all possible combinations of features.
However, we have a problem.
Calculating exact Shapley Values for machine learning models can be computationally prohibitive, as it requires evaluating all possible combinations of features. This limitation motivated the development of SHAP (SHapley Additive exPlanations).
SHAP approximates Shapley Values efficiently by leveraging sampling and other optimization techniques. This way, SHAP extends the core ideas of Shapley Values to be applicable to complex, real-world machine learning models with many features. The SHAP values remain faithful to the original Shapley Value properties and provide a practical way to interpret individual predictions.
There are different flavors of SHAP out there such as: TreeSHAP (designed for tree-based model) and DeepSHAP (designed for deep neural network).
In this essay, I will focus on Kernel SHAP, partly because it is designed to estimate Shapley values for any model (by using a specially designed kernel function, more on this later); and partly because it will be a nice continuation of the ideas in my previous essay on local surrogate model, LIME.
(Heads-up, some knowledge of LIME will make the rest of the note easier to read.)
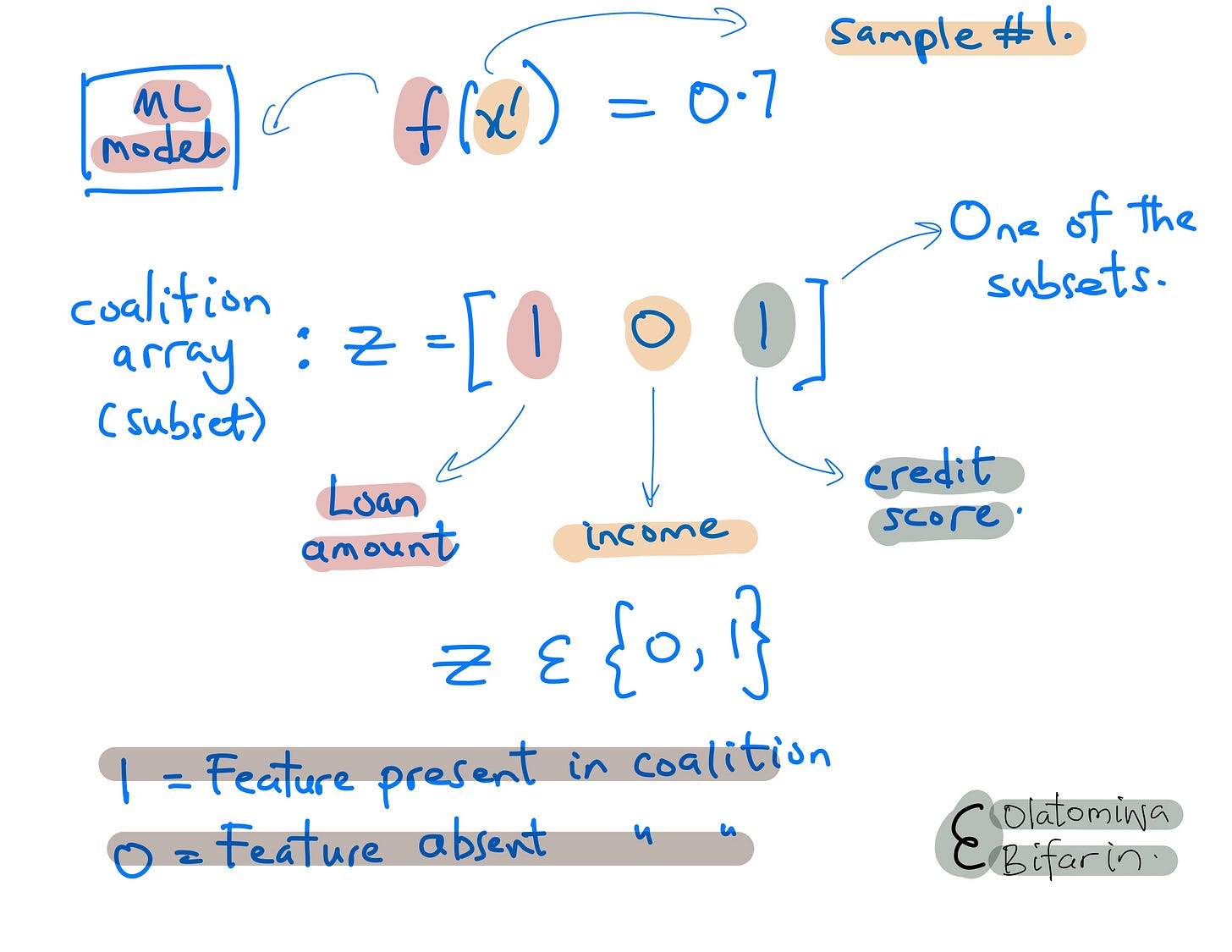
Say, I have the following dummy loan dataset.
And I want to figure out why sample #1 has her loan approved (Prb = 0.7 (>0.5)).
I do the following. First create coalition array Z.
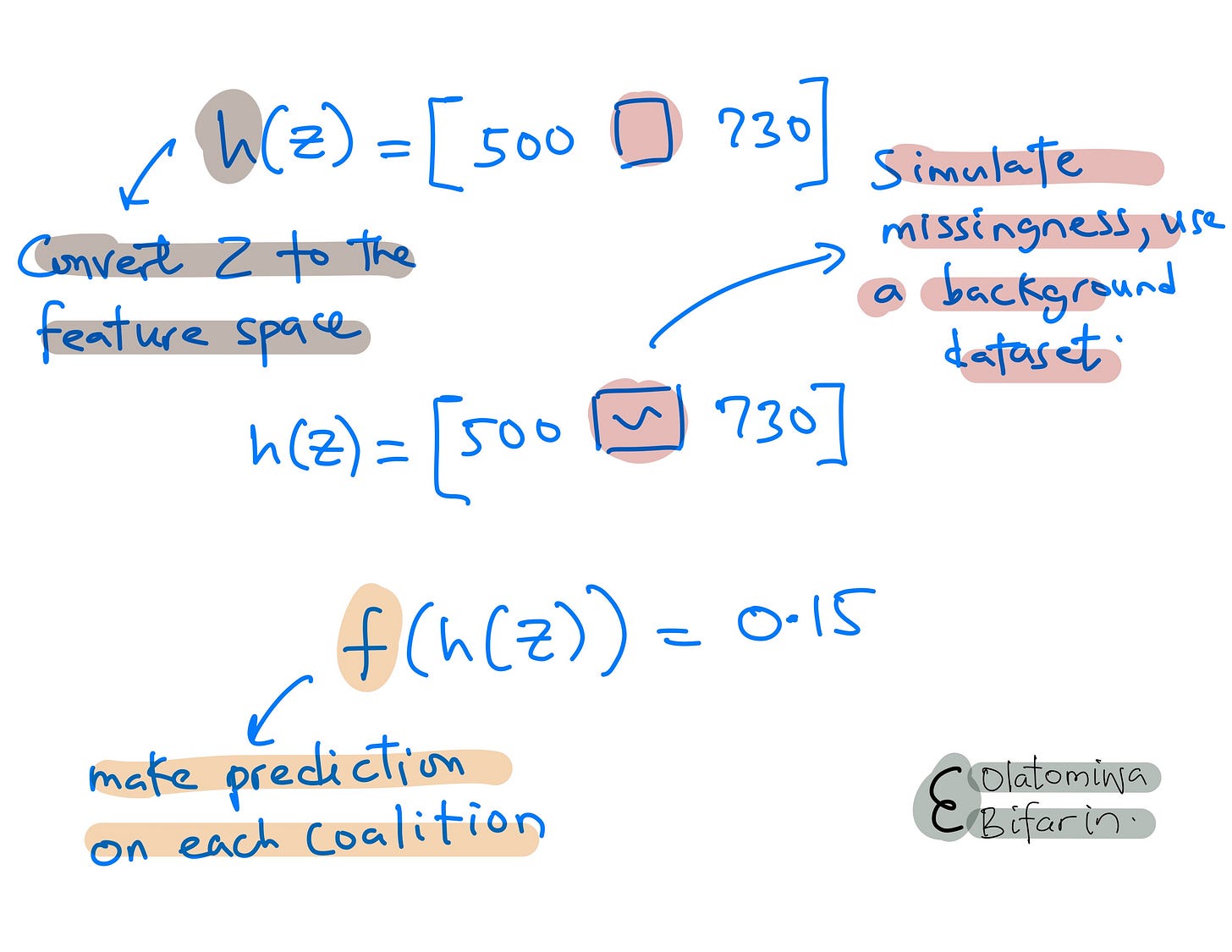
Two, get the prediction for each of the coalition array.
Three: as in Shapley values, compute the weight for each coalition with a special kernel function we can call SHAP kernel.
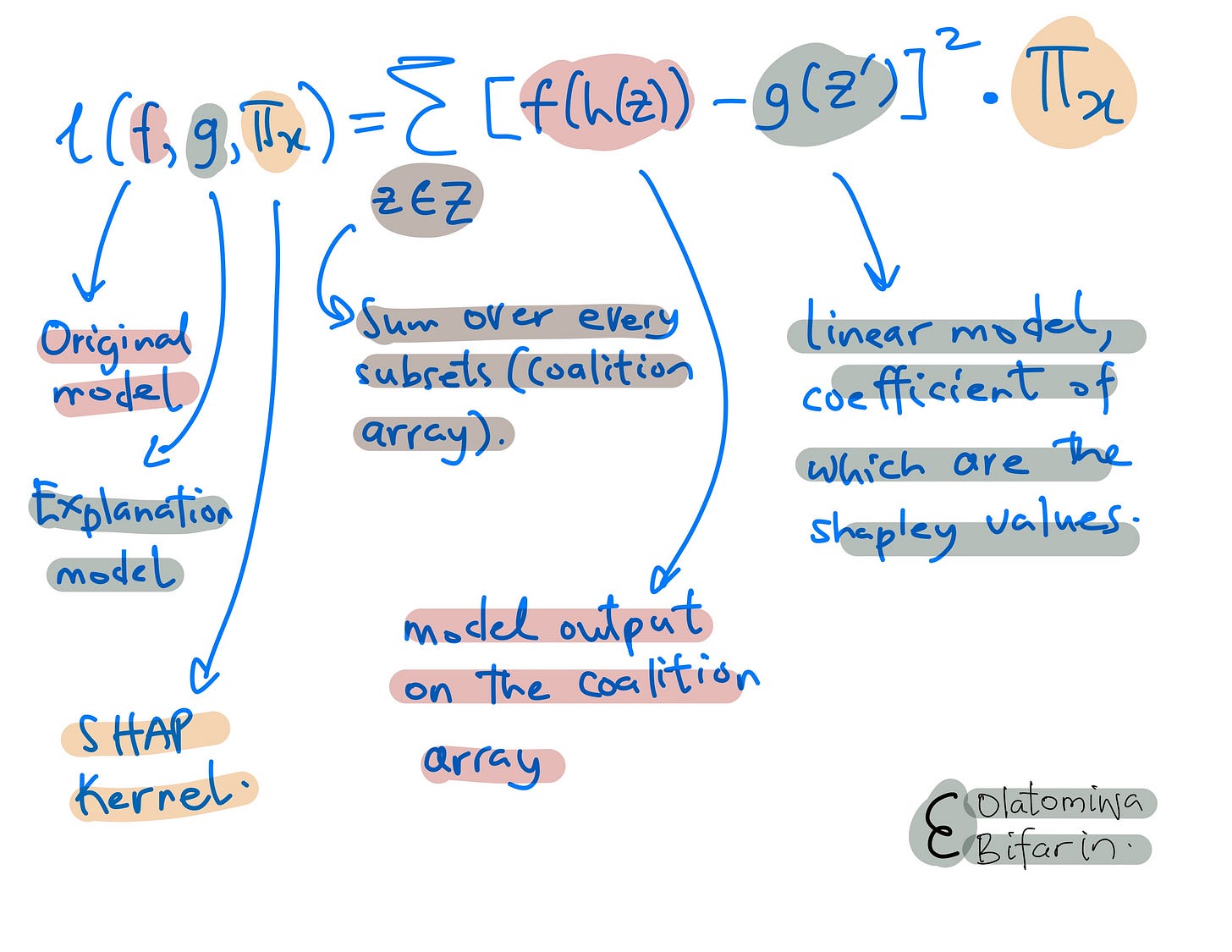
Four, we fit a weighted linear model, to get the Shapley values.
And here is the key point (also this is where we link these ideas up with LIME):
By using a weighted linear regression model as the local surrogate model and the special SHAP kernel, the regression coefficients of the (LIME) surrogate model estimates the SHAP values.
Back to the linear model.
Now that we have a function we can work with, we need a loss function that would be used to optimize the coefficient of the linear model (which, as stated earlier, in this case is our Shapley values.)
And that is the kernel SHAP in brief.
In essence, SHAP makes it possible to estimate Shapley values for complex machine learning models, something that would be computationally infeasible otherwise.
By extending ideas from game theory and using local surrogate models like LIME, SHAP brings interpretability to real-world AI systems. The additive feature contributions explain how each input drives a specific prediction.
In my next essay entry on The Epsilon, I will focus on examples of SHAP implementation with different data modalities.