Most people at this point, even those living under the proverbial rock, have used apps like chatGPT. But why are these technology so powerful? Short answer is that they use a powerful neural network architecture called Transformers.
My next series of blog on The Epsilon will be on this architecture. As such, in this blog, I write about the operation at the heart of Transformers, Self Attention.
Hope you enjoy reading.
I. The Problem with Language.
Say all we have is a fully connected neural network (FCNN) and we want to do some NLP tasks such as sentiment analysis or text generation; and we have the following sentences:
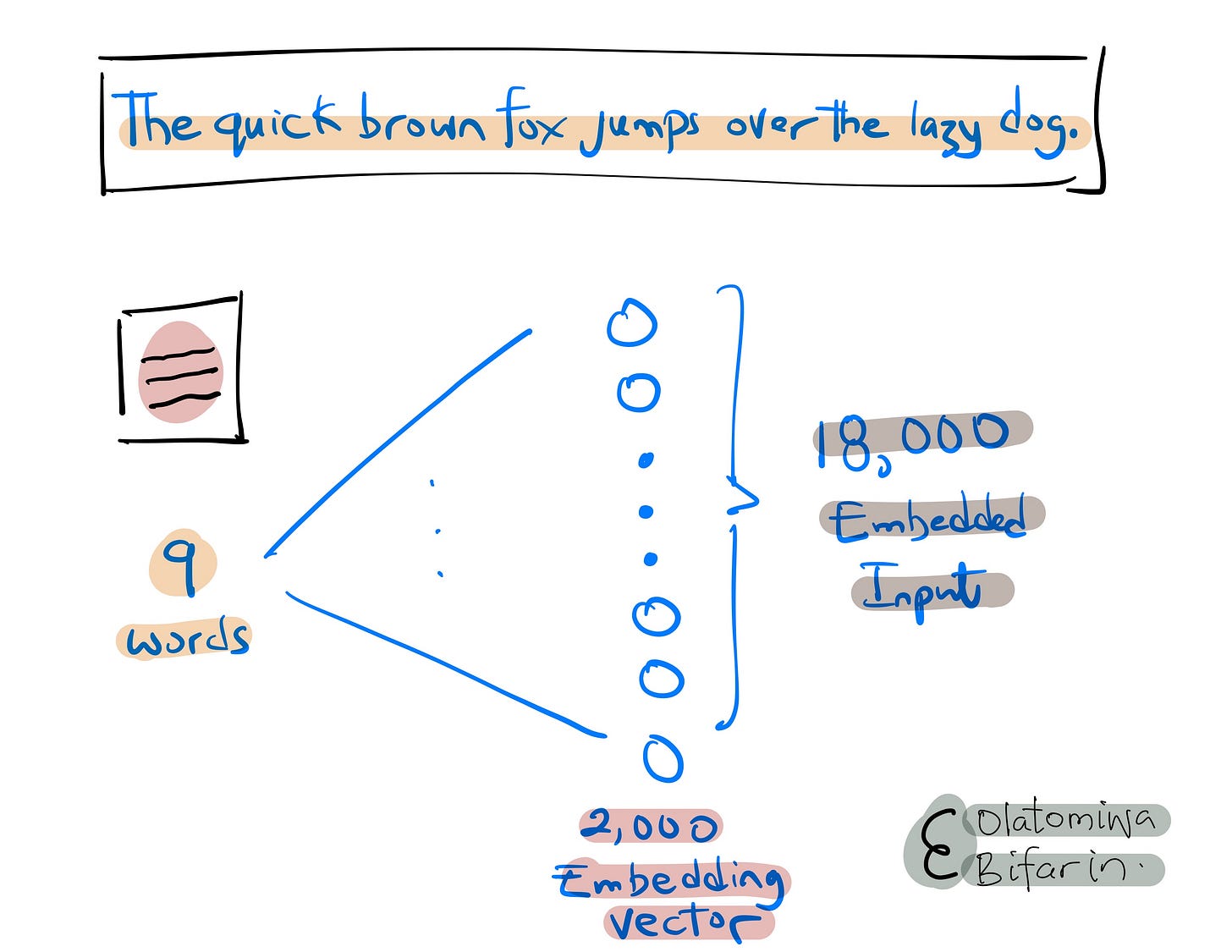
“The quick brown fox jumps over the lazy dog.”
Casting these words, admittedly naively, using FCNN with an embedding vector of length 2000 will give us an embedded input of 18,000 (9 words * 2000 dimensions per word). And this is just for a relatively short sentence. What are we going to do with paragraphs, and large corpus? Clearly FCNN, in this context, is suboptimal (computational inefficiency, overfitting).
Merge that with 1) the variable nature of inputs i.e., text lengths and 2) words depend on other words in a sentence for its meaning. Clearly, we are in need of a different neural network architecture to address this problem. Comes in attention, self-attention mechanism – the method at the heart of Transformers.
Actually, let’s go back to 1) and say a few things before moving ahead. The variable length input in NLP is an obvious problem for FCNN since they take in a fixed length input.
As such we need parameter sharing – using the same parameters (weights and biases) for more than one function in the network. We see this parameter sharing in convolutional neural networks (CNN), and recurrent neural networks (RNN).
In CNN, they apply the same sets of weight (filter) across different parts of the image.
In RNN on the other hand, they apply the same weights at each time step of the input sequence, regardless of the sequence length. This solves the problem of variable length input.
Now 2) the inherent ambiguity of words. RNN handles this with shared weights across time steps. However, this is sub-optimal for long-term dependencies due to issues like exploding and vanishing gradients.
To decisively deal with 1) and 2) Transformers uses dot-product self-attention.
Now back to attention.
II. Attention Mechanism
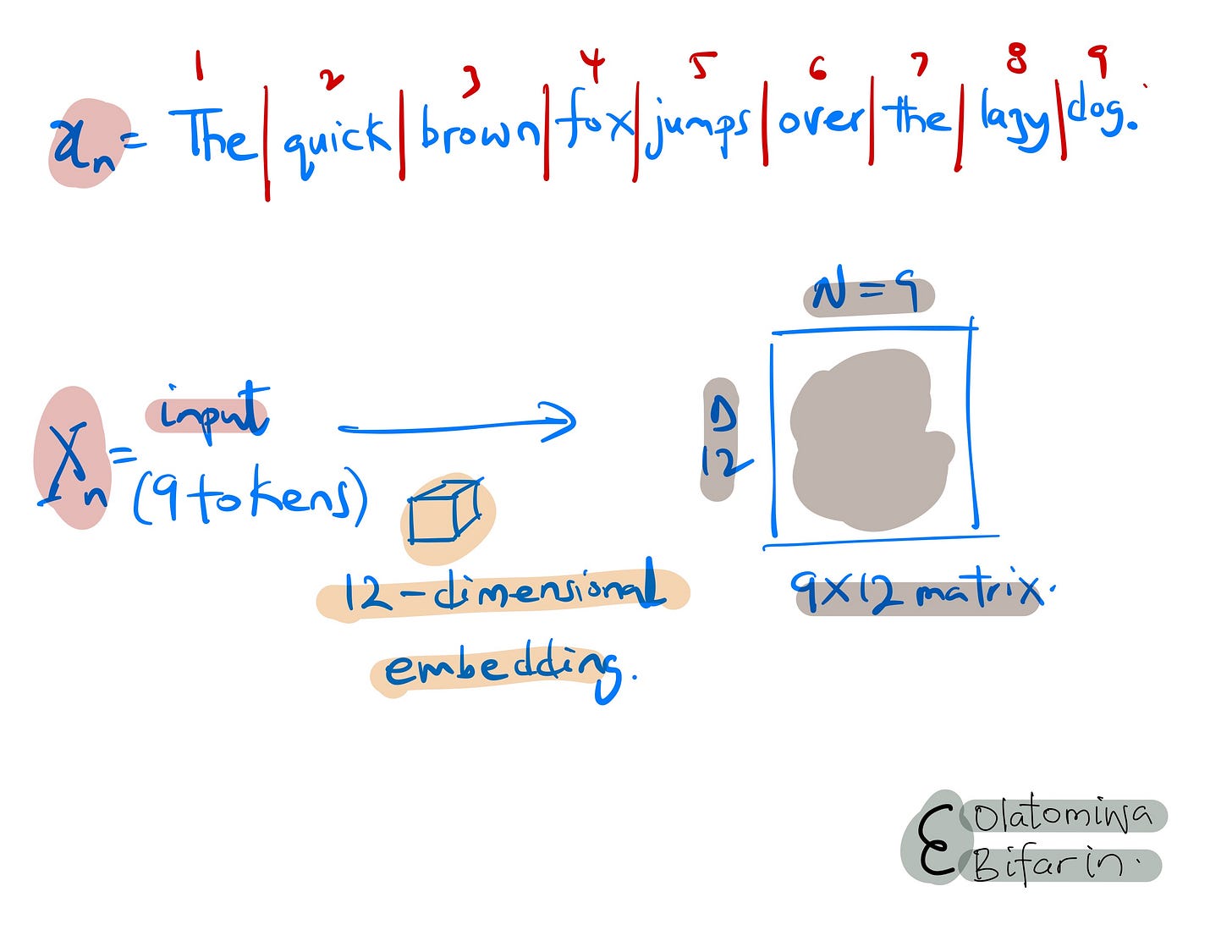
To motivate attention, we will stick to the following as our input text: “The quick brown fox jumps over the lazy dog.”
Say we split the text into 9 tokens so that N=9, following that we use a 12-dimensional embedding to generate a 9X12 vector embedding for the input tokens.
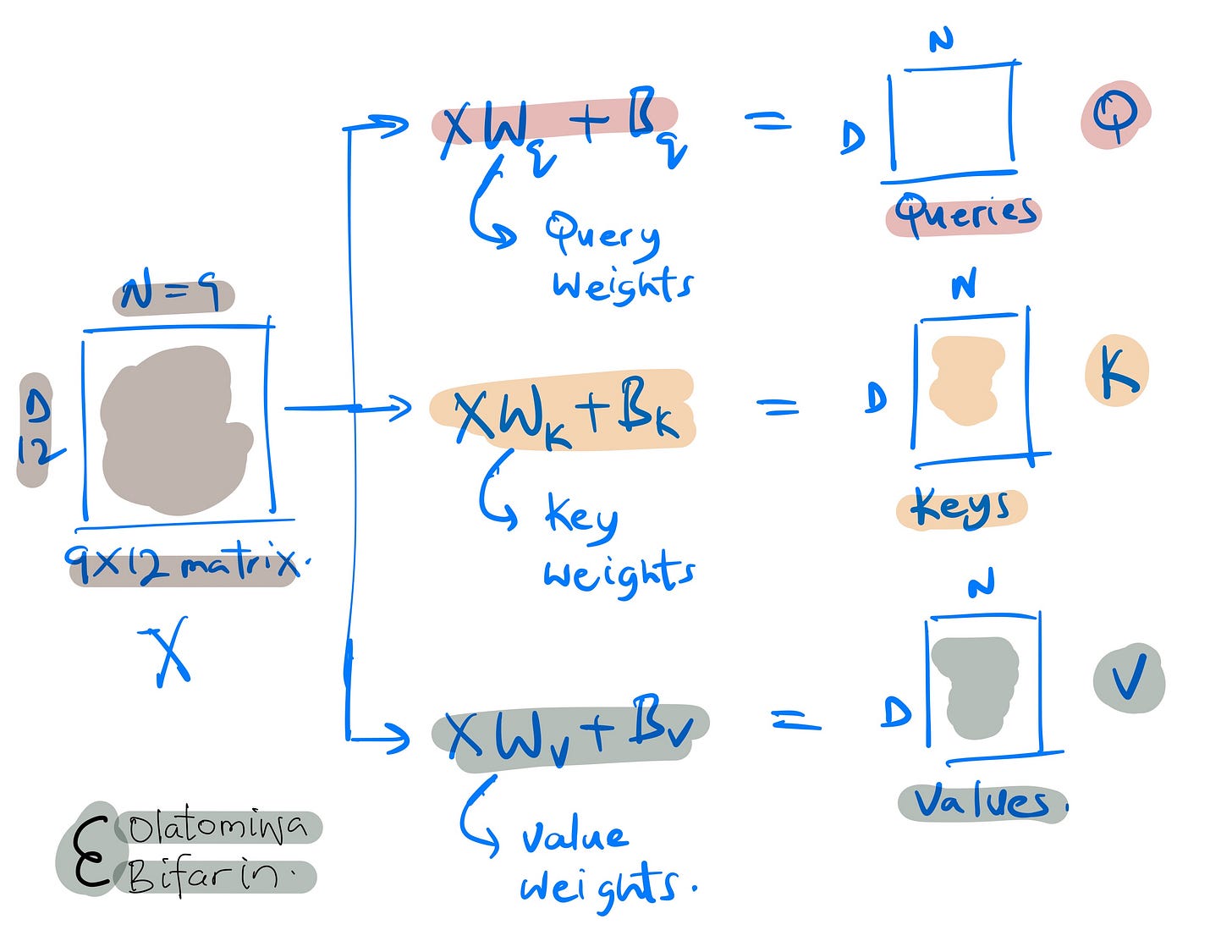
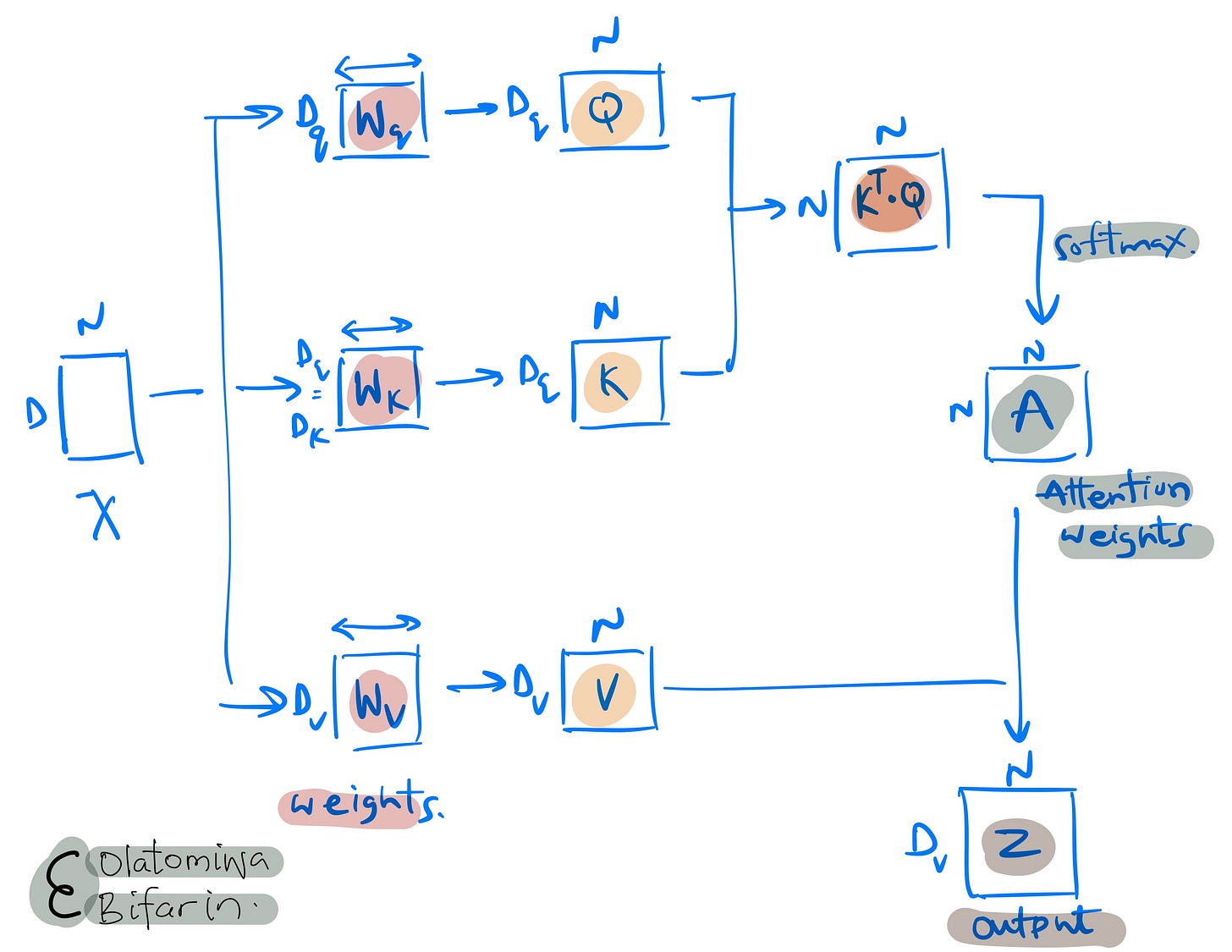
The self-attention mechanism uses three distinct sets of weights namely, 1) query weights, 2) key weights, and 3) value weights, that gives us similarly named matrices.
The terms “queries,” “keys,” and “values” in the context of self-attention mechanisms within transformer models are inspired by database terminology and are fundamental to how transformers process and interpret data.
During model training these weights (the projection matrices) are updated as they learn whatever pattern that is needed to be learnt in the data inputs.
In this stage of the computations, we are dealing with a linear transformation of the input vectors (tokens from our sentence), nothing complicated.
Perhaps this is a good junction to see what the Q, K, and V vectors will be doing in the context of the subject matter.
In brief:
Queries: This vector functions as a mechanism to evaluate the significance of various elements within the input data/tokens/words. It effectively inquires, "Which parts of these series of words hold the greatest relevance for me?"
Keys: These vectors serve the purpose of matching with the queries. Upon comparing a query with a key, the outcome tells us the relevance of the respective input component to that specific query. Here, the pertinent question is, "To what extent do I matter to each query?"
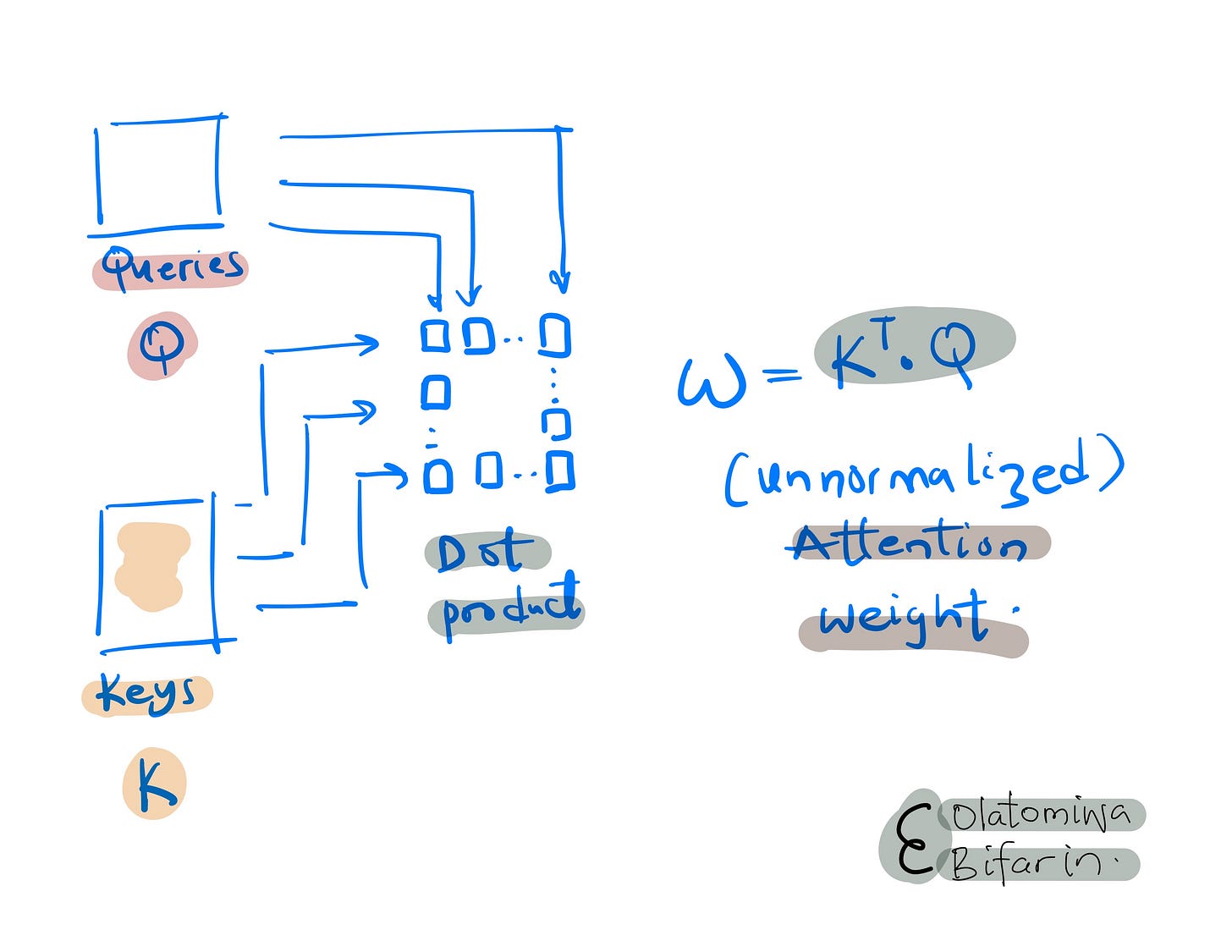
Let’s leave value vector for now, and see mathematically, what’s going on with Q and K, which in essence, is attention. To do this, first the dot product of the queries and keys is computed to give us the un-normalized attention weights.
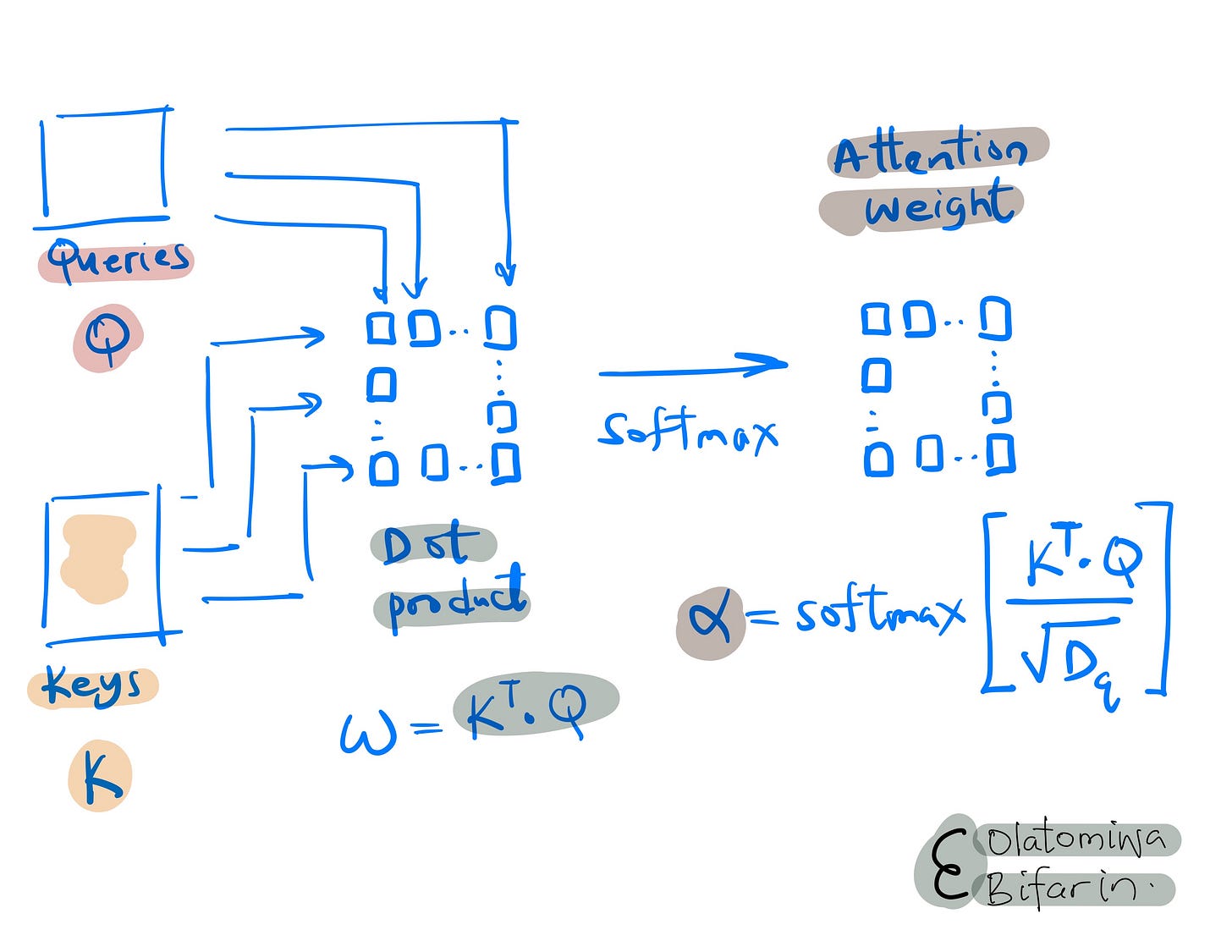
Afterwards, the results are then passed through a softmax function to give us the normalized attention weight in a process that is referred to as dot product self attention, which is indeed true to name.
Note that the softmax step normalizes the attention weights ensuring that they sum up to 1. This is important because it allows the model to distribute its focus proportionally across different parts of the input.
Additionally, the un-normalized attention scores (ω) are scaled down by a factor of 1/sqrt(d_{k}), the Euclidean length (or magnitude) of the weight vectors before applying the softmax function.
This scaling, based on the dimensionality of the keys (I skipped this part but d_{k}=d_{q}), helps to keep the magnitude of the attention weights within a reasonable range, ensuring numerical stability and aiding in effective model training.
To summarize this little bit we have been meditating on so far (Q, K, softmax, attention weights, etc):
The result of the dot product operation indicates the level of similarity between its input elements. Consequently, the weights are determined based on how similar a specific query is to each of the keys. The application of the softmax function creates this competitive dynamic among the key vectors, with each vying to influence the ultimate outcome (recall that softmax function normalizes the scores to sum up to 1).
Good.
Now let’s deal with the value vector.
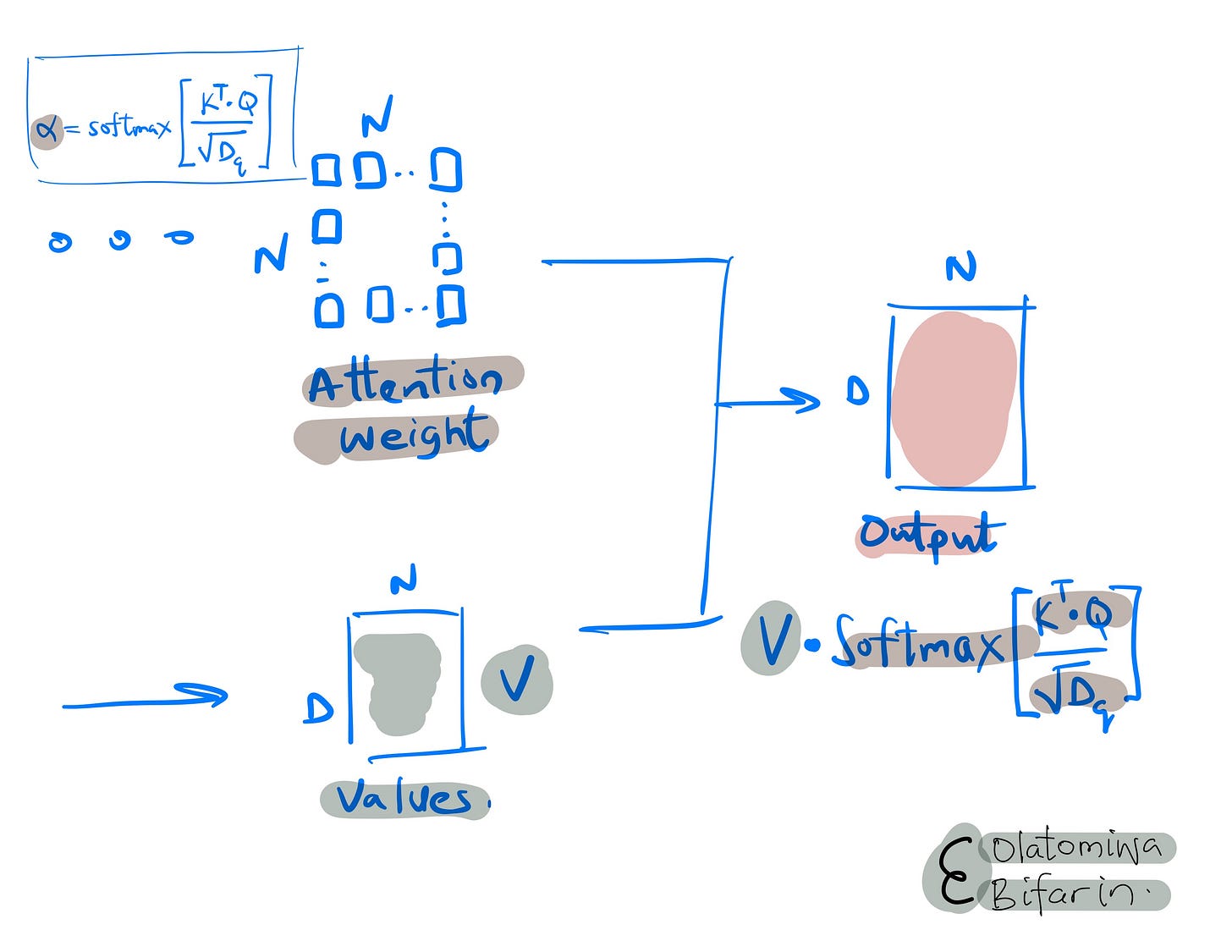
Values: In addition to queries and keys, each input element is also represented as a "value" vector. After the relevance (or attention) between elements is determined through query-key matching, these values are used to construct the output of the self-attention layer.
In essence, the value of each element is weighted by the computed attention and summed to represent the input in a new way, emphasizing the aspects that the model deems most important.
Now, let’s pull everything we have learnt so far together in one simple image.
Revisiting the previously stated requirements, which are 1) accommodating a variable number of inputs and 2) grasping the contextual significance of words, it is evident that this architecture effectively meets both criteria.
A single set of parameters (comprising the weights and biases of the query, key, and value vectors) is employed, and this remains constant regardless of the input quantity. Moreover, the implementation of attention mechanisms facilitates a contextual comprehension of word meanings.
A few more concepts and I will conclude.
III. Positional Encoding, and Multi-Head Attention
Positional encoding:
Unlike CNN and RNNs, transformers do not sequentially process inputs. And when you have such sentence as “The man beats the boy”, and “The boy beats the man.” These sentences clearly have different meanings but without a way to keep track of the sequence of input, the transformer sees no difference between them. To prevent this, Transformers use positional encoding, to incorporate positional information
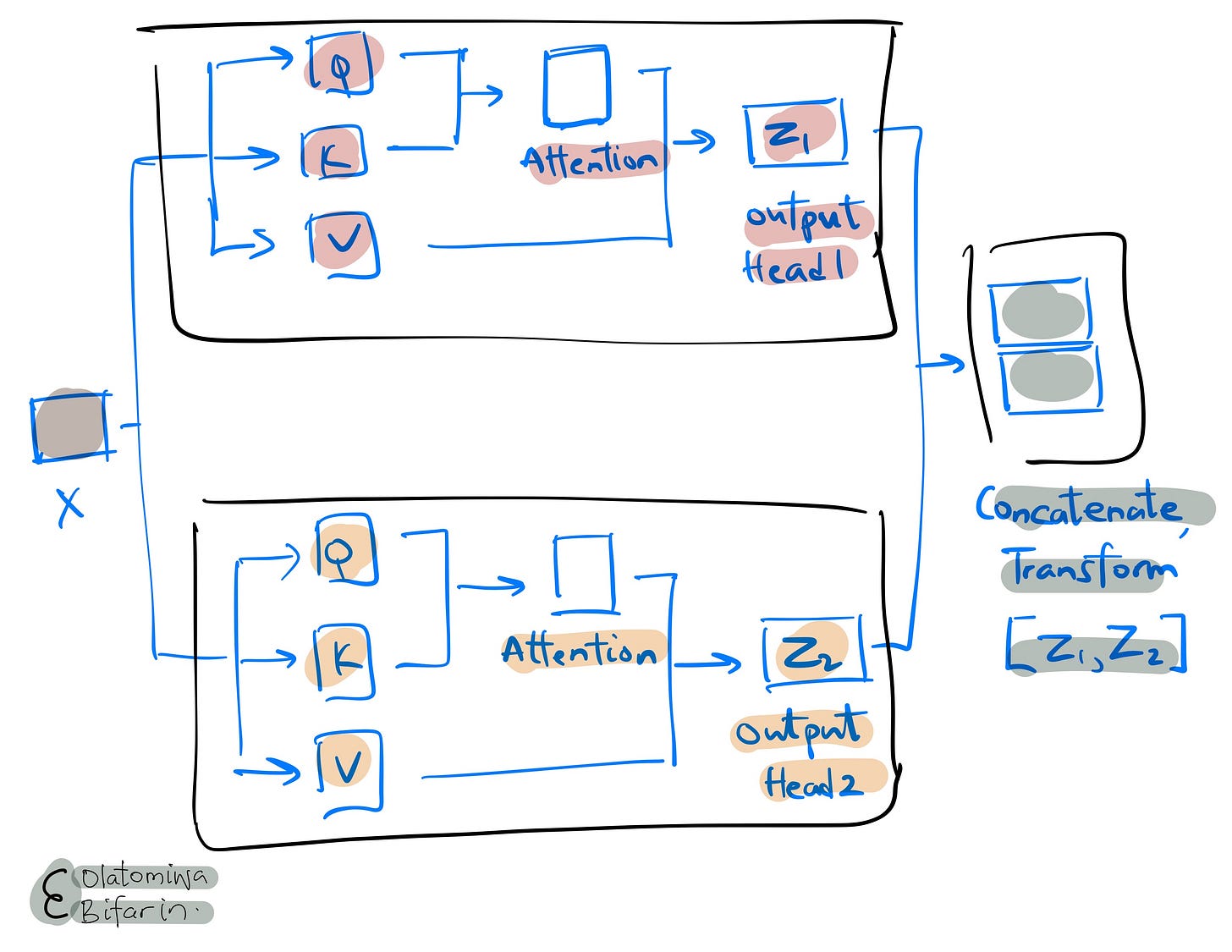
Multi-head Attention:
To make transformers work well, multiple self attention mechanism operations are run in parallel across multiple ‘heads’, with each ‘heads’ consisting of its query, key, and value matrices, and of course, all the operations that it entails. This is known as the multi-head attention.
Conceptually, this is what is going on:
To drive home the point on self attention mechanism. I encourage you to watch this one minute video by Luis Serrano.
IV. Conclusion
In summary, self-attention mechanisms mark a significant advancement in neural network architectures. There is no need for advertisements, technologies like chatGPT are testaments to their powers.
However, self attention is just one part of the Transformer architecture, so looking ahead, my next blog will delve into the transformer architecture, building upon these concepts to showcase its profound impact on AI applications.
References
Understanding Deep Learning by Simon Prince Chapter on Transformers.
Understanding and Coding the Self-Attention Mechanism of Large Language Models From Scratch by Sebastian Raschka.